ସମଦ୍ୱିବାହୁ ତ୍ରିଭୁଜ
| Isosceles triangle | |
|---|---|
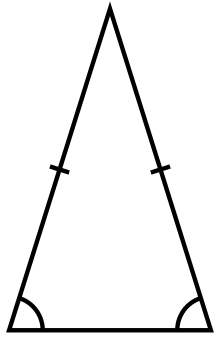 Isosceles triangle with vertical axis of symmetry | |
| Type | triangle |
| Edges and vertices | 3 |
| Schläfli symbol | ( ) ∨ { } |
| Symmetry group | Dih2, [ ], (*), order 2 |
| Dual polygon | Self-dual |
| Properties | convex, cyclic |
ଜ୍ୟାମିତିରେ ସମଦ୍ୱିବାହୁ ତ୍ରିଭୁଜ କହିଲେ ଦୁଇଟି ସମାନ ଲମ୍ବ ବିଶିଷ୍ଟ ବାହୁ ଥିବା ତ୍ରିଭୁଜକୁ ବୁଝାଏ । ବେଳେ ବେଳେ ଅତି କମ୍ରେ ଦୁଇଟି ବାହୁ ସମାନ ଥିବା କୁହାଯାଏ ଓ ସେହି କ୍ଷେତ୍ରରେ ଏହା ସମବାହୁ ତ୍ରିଭୁଜ ମଧ୍ୟ ହୋଇପାରେ । ସମଦ୍ୱିବାହୁ ତ୍ରିଭୁଜ ଉଦାହରଣ ମଧ୍ୟରେ ସମଦ୍ୱିବାହୁ ସମକୋଣୀ ତ୍ରିଭୁଜ, ସ୍ୱର୍ଣ୍ଣିମ ତ୍ରିଭୁଜ (golden triangle) ଓ ବାଇପିରାମିଡର (bipyramids) ମୁଖ ଓ କେତେକ ସେଟାଲାନ ଘନ (Catalan solids) ଉଲ୍ଲେଖନୀୟ ।
ସମଦ୍ୱିବାହୁର ଗାଣିତିକ ଅନୁଶୀଳନ ପୁରାତନ ମିଶର ଗଣିତ (ancient Egyptian mathematics) ଓ ବେବିଲୋନିଆନ ଗଣିତରେ (Babylonian mathematics) ଲିପିବଦ୍ଧ ହୋଇଛି । ସାଜସଜ୍ଜା ନିମନ୍ତେ ଏହା ବହୁତ ପୁରାତନ କାଳରୁ ବ୍ୟବହୃତ ହେଉଛି; ସ୍ଥାପତ୍ୟ କଳା ଓ ନକ୍ସାରେ ଏହା ପୁନଃ ପୁନଃ ବ୍ୟବହାର କରାଯାଉଛି ଯେପରିକି ବିଲ୍ଡିଙ୍ଗର ପେଡିମେଣ୍ଟ (pediments) ଓ ଗ୍ୟାବଲରେ (gables) ଅଛି ।
ସମାନ ଥିବା ଦୁଇ ପାର୍ଶକୁ ବାହୁ କୁହାଯାଏ ଓ ତୃତୀୟ ପାର୍ଶ୍ୱକୁ ବେସ କୁହାଯାଏ । ବାହୁ ଓ ବେସର ଦୈର୍ଘ୍ୟକୁ ନେଇ ଏପରି ତ୍ରିଭୁଜର ଉଚ୍ଚତା, କ୍ଷେତ୍ରଫଳ ଓ ପେରିମିଟର ଇତ୍ୟାଦି ସାଧାରଣ ଫର୍ମୁଲା ସାହାଯ୍ୟରେ ନିର୍ଣ୍ଣୟ କରାଯାଇପାରେ । ବେସ ଉପରେ ଏକ ଅଭିଲମ୍ବ ରେଖା (perpendicular bisector) ଟାଣି ଏହି ତ୍ରିଭୁଜକୁ ସମାନ ଦୁଇ ଖଣ୍ଡରେ ବିଭକ୍ତ କରାଯାଇପାରେ । ସମଦ୍ୱିବାହୁର ବିପରୀତ ଦିଗରେ ଥିବା କୋଣଦ୍ୱୟ ସମାନ ଓ ଆକ୍ୟୁଟ ରହନ୍ତି ଓ ବର୍ଗୀକରଣରେ ଏହାକୁ ଆକ୍ୟୁଟ, ସମ ବା ବିଷମ କୋଣ ବିଶିଷ୍ଟ କୁହାଯାଏ ।
ଶବ୍ଦ ବିଶେଷ, ବର୍ଗୀକରଣ ଓ ଉଦାହରଣ
[ସମ୍ପାଦନା]ଇଉକ୍ଲିଡଙ୍କ (Euclid) ସଂଜ୍ଞା ଅନୁସାରେ ତ୍ରିଭୁଜର ଦୁଇଟି ବାହୁ ସମ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ହୋଇଥିଲେ ସମଦ୍ୱିବାହୁ ତ୍ରିଭୁଜ କୁହାଯାଏ, [୧] କିନ୍ତୁ ଆଧୁନିକ ସମୟରେ ଅତି କମ୍ରେ ଦୁଇଟି ବାହୁ ସମ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ହୋଇଥିଲେ ସମଦ୍ୱିବାହୁ ତ୍ରିଭୁଜ କୁହାଯାଉଛି । ଏହାର କାରଣ ରୂପେ ସମବାହୁ ତ୍ରିଭୁଜକୁ ଏକ ବିଶେଷ ଧରଣର ସମଦ୍ୱିବାହୁ ତ୍ରିଭୁଜ ଭାବରେ ଗ୍ରହଣ କରାଯାଉଛି ।[୨] ତ୍ରିଭୁଜର କୌଣସି ବାହୁ ସମ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ନହେଲେ ତାହାକୁ ସ୍କାଲିନି ତ୍ରିଭୁଜ scalene ବା ବିଷମ ବାହୁ ତ୍ରିଭୁଜ କୁହାଯାଏ । [୩] ଗ୍ରୀକ୍ ଭାଷାରେ ଆଇସୋସ ଅର୍ଥ ସମାନ ଓ ସ୍କେଲୋସ ଅର୍ଥ ଗୋଡ଼, କିନ୍ତୁ ଆମେ ତାହାକୁ ବାହୁ ଭାବରେ ଲେଖୁଛୁ । ସମଦ୍ୱିବାହୁ ଶବ୍ଦ ଅନ୍ୟ ସ୍ଥାନରେ ମଧ୍ୟ ବ୍ୟବହାର ହେଉଛି ଯଥା ସମଦ୍ୱିବାହୁ ଟ୍ରାପିଜଏଡ଼ ଯାହାର ଦୁଇଟି ବାହୁ ସମାନ ଥାଏ [୪] ଓ ସମବାହୁ ସେଟ । [୫]
ଏକ ସମଦ୍ୱିବାହୁ ତ୍ରିଭୁଜରେ ଦୁଇଟି ରେଖାର ଦୈର୍ଘ୍ୟ ସମାନ ରହେ, ଯାହାକୁ ଜ୍ୟାମିତିରେ ବାହୁ କୁହାଯାଉଛି ଓ ତୃତୀୟ ବାହୁକୁ ଭୂମି କୁହାଯାଉଛି । ଦୁଇ ବାହୁ ମଧ୍ୟସ୍ଥ କୋଣକୁ ଶୀର୍ଷ କୋଣ କୁହାଯାଏ । ଭୂମିର ଦୁଇ ପର୍ଶ୍ୱରେ ଥିବା କୋଣମାନଙ୍କୁ ଭୂମି କୋଣ କୁହାଯାଏ । [୬] ଭୂମିର ବିପରୀତ ସ୍ଥାନକୁ ଶୀର୍ଷ କୁହାଯାଏ (apex) ।[୭] ତିନି ବାହୁ ସମାନ ଥିବାରୁ ସମବାହୁ ତ୍ରିଭୁଜର ଭୂମି ନଥାଏ । [୮]
ପ୍ରୟୋଗ
[ସମ୍ପାଦନା]In architecture and design
[ସମ୍ପାଦନା]ସ୍ଥାପତ୍ୟରେ ଏହାର ପ୍ରୟୋଗ ଦେଖିବାକୁ ମିଳେ । ପୁରାତନ ଗ୍ରୀକ ସ୍ଥାପତ୍ୟରେ (architecture) ଓ ପରବର୍ତ୍ତୀ କାଳରେ ସ୍ଥୁଳ କୋଣ ବିଶିଷ୍ଟ ସମଦ୍ୱିବାହୁ ତ୍ରିଭୁଜ ଭଳି ଆକାର (gables ଓ pediment) ଦେଖିବାକୁ ମିଳେ । ଗୋଥିକ ସ୍ଥାପତ୍ୟରେ (Gothic architecture) ଏହା ସୁକ୍ଷ୍ମ କୋଣ ବିଶିଷ୍ଟ ଆକାର ଧାରଣ କଲା । [୮]

ଆଧାର
[ସମ୍ପାଦନା]- ↑ Heath (1956), p. 187, Definition 20.
- ↑ Stahl (2003), p. 37.
- ↑ Usiskin & Griffin (2008), p. 4.
- ↑ Usiskin & Griffin (2008), p. 41.
- ↑ Ionin (2009).
- ↑ Jacobs (1974), p. 144.
- ↑ Gottschau, Haverkort & Matzke (2018).
- ↑ ୮.୦ ୮.୧ Lardner (1840), p. 46.


