ଡୋପ୍ଲର୍ ପ୍ରଭାବ

ଉତ୍ସର ଗତି ଯୋଗୁଁ ତରଙ୍ଗର ଦୈର୍ଘ୍ୟରେ ପରିବର୍ତ୍ତନ ଦେଖାଯାଏ

ଡୋପ୍ଲର୍ ପ୍ରଭାବ ଦର୍ଶାଉଥିବା ଏକ କମ୍ପ୍ୟୁଟର୍ ଆନିମେସନ୍ । ଗୋଲାପୀ ବୃତ୍ତଗୁଡ଼ିକ ଶବ୍ଦ ତରଙ୍ଗକୁ ସୂଚାଉଛନ୍ତି । ଉତ୍ସ ଶ୍ରୋତା ପାଖକୁ ଆସିବା ବେଳେ ସାଇରନ୍ ଶବ୍ଦର ତୀବ୍ରତା ବା ତାରତ୍ୱ ବଢ଼େ ଓ ଦୂରକୁ ଗଲେ ତୀବ୍ରତା କମେ ।

ତରଙ୍ଗ ଉତ୍ସ ଓ ଦେଖଣାହାରୀ ବା ଶ୍ରୋତା ମଧ୍ୟରେ ଆପେକ୍ଷିକ ଗତି ରହିଥିଲେ ତରଙ୍ଗର ଦୈର୍ଘ୍ୟ ବା ଆବୃତ୍ତିରେ ପରିବର୍ତ୍ତନ ଘଟି ଯେଉଁ ପ୍ରଭାବ ଅନୁଭୂତ ହୁଏ ତାହାକୁ ଡୋପ୍ଲର୍ ପ୍ରଭାବ (ଈଂରାଜୀରେ Doppler Effect) ବା ଡୋପ୍ଲର୍ ବିସ୍ଥାପନ (ଈଂରାଜୀରେ Doppler Shift) କୁହାଯାଏ । ଅଷ୍ଟ୍ରିଆ ଦେଶର ପଦାର୍ଥ ବିଜ୍ଞାନୀ ଖ୍ରୀଷ୍ଟିୟାନ୍ ଡୋପ୍ଲର୍ ୧୮୪୨ ମସିହାରେ ଏହି ପ୍ରଭାବ ବିଷୟରେ ପ୍ରଥମେ ବୈଜ୍ଞାନିକ ବର୍ଣ୍ଣନା ଦେଇଥିବାରୁ ଏହାର ଏପରି ନାମକରଣ ହୋଇଛି ।

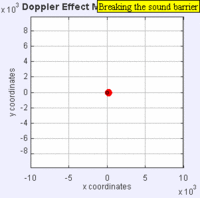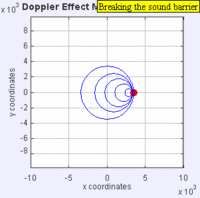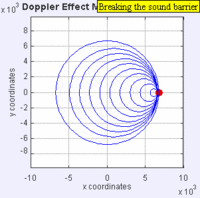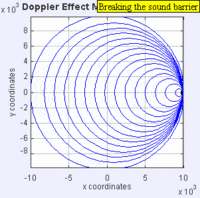
ଉଦାହରଣ ସ୍ୱରୂପ : ମନେ କରାଯାଉ ଯେ ଏକ ଗାଡ଼ି ସାଇରନ୍ ବଜାଇ ଆମ ଆଡ଼କୁ ଆସୁଛି । ଆମ ଆଡ଼କୁ ଗାଡ଼ିଟି ଆସିବା ବେଳେ ତାର ସାଇରନ୍ ଶବ୍ଦର ତାରତ୍ୱ (Pitch) ବା ଧ୍ୱନିର ତୀବ୍ରତା କ୍ରମଶଃ ବଢ଼ିଲା ପରି ଅନୁଭୂତ ହୁଏ । କିନ୍ତୁ ଗାଡ଼ିଟି ଆମକୁ ଅତିକ୍ରମ କରି ଦୂରକୁ ଯିବାବେଳେ ତାହାର ସାଇରନ୍‍ର ତୀବ୍ରତା ବା ତାରତ୍ୱ କମିଯିବା ପରି ଲାଗେ । ତେଣୁ ଧ୍ୱନି ତରଙ୍ଗ ଉତ୍ସ ଶ୍ରୋତା ଆଡ଼କୁ ଯାଉଥିବା ସମୟରେ ପରିଲକ୍ଷିତ ଆବୃତ୍ତି ପ୍ରକୃତ ଆବୃତ୍ତିଠାରୁ ଅଧିକ ଜଣାପଡ଼େ ଓ ଅପରପକ୍ଷେ ଧ୍ୱନି ଉତ୍ସ ଶ୍ରୋତାଠାରୁ ଦୂରକୁ ଯାଉଥିବା ସମୟରେ ପରିଲକ୍ଷିତ ଆବୃତ୍ତି ପ୍ରକୃତ ଆବୃତ୍ତିଠାରୁ କମ୍ ଥିବା ପରି ଜଣାପଡ଼େ । ଉତ୍ସରୁ ବାହାରୁଥିବା ତରଙ୍ଗ ଶିଖର ଗହ୍ୱର ଆକାରରେ ସଦା ସର୍ବଦା ଶ୍ରୋତା ଆଡ଼କୁ ଗତି କରୁଥାନ୍ତି । ଉତ୍ସ ଶ୍ରୋତା ଆଡ଼କୁ ଗତି କଲେ ପରବର୍ତ୍ତୀ ତରଙ୍ଗ ଶିଖରଗୁଡ଼ିକ ପୂର୍ବାପେକ୍ଷା ଶ୍ରୋତାର ଆହୁରି ନିକଟତର ସ୍ଥାନରୁ ଶ୍ରୋତା ଆଡ଼କୁ ଗତି କରନ୍ତି । ଏହା ଫଳରେ ପ୍ରତ୍ୟେକ ତରଙ୍ଗକୁ ଶ୍ରୋତା ପାଖରେ ପହଞ୍ଚିବାକୁ କମ୍ ସମୟ ଲାଗେ । ଶ୍ରୋତା ନିକଟରେ ପହଞ୍ଚୁଥିବା ବିଭିନ୍ନ ତରଙ୍ଗ ମଧ୍ୟରେ ବେଶୀ ସମୟ ବ୍ୟବଧାନ ରହେ ନାହିଁ ଓ ତରଙ୍ଗର ଆବୃତ୍ତି ବଢ଼ିଯାଏ । ତେଣୁ ତରଙ୍ଗ ଗୁଡ଼ିକ ଏକାଠି ହୋଇଯାନ୍ତି ଓ ତୀବ୍ରତା ବୃଦ୍ଧି ପାଏ । ଉତ୍ସ ଶ୍ରୋତାଠାରୁ ଦୂରକୁ ଗଲାବେଳେ ପରବର୍ତ୍ତୀ ତରଙ୍ଗଗୁଡ଼ିକ ଅଧିକ ଦୂରତାରୁ ସୃଷ୍ଟି ହୁଅନ୍ତି, ତେଣୁ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ତରଙ୍ଗ ଓ ତାହାର ପରବର୍ତ୍ତୀ ତରଙ୍ଗ ପହଞ୍ଚିବା ମଧ୍ୟରେ ଅନେକ ସମୟ ବ୍ୟବଧାନ ରହିଯାଏ । ଏହା ଫଳରେ ତରଙ୍ଗଗୁଡ଼ିକ ଦୂରେଇଯାନ୍ତି ଓ ତୀବ୍ରତା ହ୍ରାସ ପାଏ । ଏହା ହିଁ ଡୋପ୍ଲର୍ ପ୍ରଭାବର କାରଣ ।

ଏକ ମାଧ୍ୟମ ଦେଇ ଗତି କରୁଥିବା ତରଙ୍ଗ ପାଇଁ ଉତ୍ସର ମାଧ୍ୟମ ସହିତ ଆପେକ୍ଷିକ ବେଗ ଓ ଶ୍ରୋତାର ମାଧ୍ୟମ ସହିତ ଆପେକ୍ଷିକ ବେଗ ନିର୍ଣ୍ଣୟ କରିବା ଜରୁରୀ । ଉତ୍ସ ଗତିଶୀଳ ଥିଲେ ବା ଶ୍ରୋତା ଗତିଶୀଳ ଥିଲେ ବା ତରଙ୍ଗର ମାଧ୍ୟମ ଗତି କରୁଥିଲେ - ଏପରି ଅନେକ କାରଣ ଯୋଗୁଁ ଡୋପ୍ଲର୍ ପ୍ରଭାବ ସୃଷ୍ଟି ହୋଇପାରେ । ଆଲୋକ ପରି ବିଦ୍ୟୁତ୍-ଚୁମ୍ବକୀୟ ତରଙ୍ଗ ବା ମହାକର୍ଷଣୀୟ ତରଙ୍ଗ ସଞ୍ଚାରିତ ହେବା ପାଇଁ କୌଣସି ମାଧ୍ୟମର ଆବଶ୍ୟକତା ନଥାଏ । ଏପରି ସ୍ଥିତିରେ କେବଳ ଉତ୍ସ ଓ ଦେଖଣାହାରୀର ଆପେକ୍ଷିକ ଗତି ଜାଣିବା ଆବଶ୍ୟକ ।

ଇତିହାସ

୧୮୪୨ ମସିହାରେ ଖ୍ରୀଷ୍ଟିୟାନ୍ ଡୋପ୍ଲର୍ ଜର୍ମାନ୍ ଭାଷାରେ “Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels” (ଅର୍ଥାତ୍ – ଦ୍ୱୈତ ତାରକା ଓ ସ୍ୱର୍ଗର ଅନ୍ୟ କିଛି ତାରକାଙ୍କ ରଙ୍ଗୀନ ଆଲୋକ ବିଷୟରେ) ନାମକ ଏକ ନିବନ୍ଧ ଲେଖିଥିଲେ । ୧୮୪୫ ମସିହାରେ ବୁଏ ବେଲୋ ଧ୍ୱନି ତରଙ୍ଗ ସହାୟତାରେ ଏହି ନିବନ୍ଧ ସମ୍ପର୍କିତ ପରୀକ୍ଷା କରିଥିଲେ । ଶବ୍ଦର ଉତ୍ସ ତାଙ୍କ ଆଡ଼କୁ ଆସିବା ବେଳେ ଶବ୍ଦର ତୀବ୍ରତା ବଢ଼ୁଥିବା ଓ ଉତ୍ସ ଦୂରକୁ ଯିବାବେଳେ ତୀବ୍ରତା କମୁଥିବା ବିଷୟକୁ ସେ ସ୍ୱୀକାର କଲେ । ୧୮୪୮ ମସିହାରେ ହିପୋଲୈଟ୍ ଫିଜ୍ୟୁ ନିଜ ସ୍ୱତନ୍ତ୍ର ପରୀକ୍ଷାରେ ବିଦ୍ୟୁତ୍-ଚୁମ୍ବକୀୟ ତରଙ୍ଗ ପାଇଁ ଏପରି ପ୍ରଭାବ ଦେଖାଯିବା ପ୍ରକାଶ କରିଥିଲେ କିନ୍ତୁ ଫିଜ୍ୟୁଙ୍କ ଆବିଷ୍କାର ଡୋପ୍ଲର୍‍ଙ୍କ ଆବିଷ୍କାରର ୬ ବର୍ଷ ପରେ ଆସିଥିବାରୁ ଏହି ପ୍ରଭାବ ସହିତ ଫିଜ୍ୟୁଙ୍କ ନାମ ଯୋଡ଼ା ଗଲାନାହିଁ । ଅବଶ୍ୟ କେହି କେହି ଏହାକୁ “effet Doppler-Fizeau” ବୋଲି ମଧ୍ୟ କହିଥାନ୍ତି କିନ୍ତୁ ଏହି ନାମଟି ସର୍ବଗୃହୀତ ନୁହେଁ । ୧୮୪୮ ମସିହାରେ ବ୍ରିଟେନ୍‍ରେ ଜନ୍ ସ୍କଟ୍ ରସେଲ୍ ଡୋପ୍ଲର୍ ପ୍ରଭାବ ବିଷୟରେ ଅଧିକ ପରୀକ୍ଷଣ କରିଥିଲେ ।

ସାଧାରଣ ତଥ୍ୟ

ପାରମ୍ପରିକ ପଦାର୍ଥ ବିଜ୍ଞାନରେ ତରଙ୍ଗ ଉତ୍ସ ବା ଶ୍ରୋତା ଓ ମାଧ୍ୟମ ମଧ୍ୟରେ ରହିଥିବା ଆପେକ୍ଷିକ ବେଗ ତରଙ୍ଗର ବେଗ ଅପେକ୍ଷା କମ୍ ହୋଇଥିବାରୁ ପରିଲକ୍ଷିତ ଆବୃତ୍ତି $f$ ଓ ପ୍ରକୃତ ଆବୃତ୍ତି $f_{\text{0}}$ ମଧ୍ୟରେ ରହିଥିବା ସମ୍ପର୍କକୁ ନିମ୍ନ ପ୍ରକାରରେ ଲେଖାଯାଇପାରିବ :

$f=\left({\frac {c+v_{\text{r}}}{c+v_{\text{s}}}}\right)f_{0}\,$

ଏଠାରେ

$c\;$ ମାଧ୍ୟମରେ ତରଙ୍ଗର ବେଗକୁ ସୂଚିତ କରେ;

$v_{\text{r}}\,$ ଶ୍ରୋତା ବା ଦେଖଣାହାରୀ ଓ ମାଧ୍ୟମ ମଧ୍ୟରେ ରହିଥିବା ଆପେକ୍ଷିକ ବେଗକୁ ସୂଚିତ କରେ (ଶ୍ରୋତା ତରଙ୍ଗ ଉତ୍ସ ଆଡ଼କୁ ଗତି କରୁଥିଲେ ଏହାର ମାନ ଯୁକ୍ତ ଓ ଉତ୍ସରୁ ଦୂରକୁ ଗତି କରୁଥିଲେ ଏହାର ମାନ ବିଯୁକ୍ତ ହୋଇଥାଏ) ;

$v_{\text{s}}\,$ ଉତ୍ସ ଓ ମାଧ୍ୟମ ମଧ୍ୟରେ ରହିଥିବା ଆପେକ୍ଷିକ ବେଗକୁ ସୂଚାଏ (ଉତ୍ସ ଶ୍ରୋତା ଆଡ଼କୁ ଗତି କରୁଥିଲେ ଏହାର ମାନ ବିଯୁକ୍ତ ଓ ଶ୍ରୋତାରୁ ଦୂରକୁ ଗତି କରୁଥିଲେ ଏହାର ମାନ ଯୁକ୍ତ ହୋଇଥାଏ) ।

ଉତ୍ସ ବା ଶ୍ରୋତା ପରସ୍ପରଠାରୁ ଦୂରକୁ ଯାଉଥିଲେ ଆବୃତ୍ତି ହ୍ରାସ ପାଇଥାଏ ।

ଉପରୋକ୍ତ ସୂତ୍ରରେ ଉତ୍ସର ଗତିର ରେଖା ଉପରେ ଶ୍ରୋତା ରହିଥିବାର ଧାରଣା କରାଯାଇଛି । ଯଦି ଉତ୍ସର ସରଳ ରୈଖିକ ଗତିପଥ ଓ ଶ୍ରୋତାର ଅବସ୍ଥିତି ମଧ୍ୟରେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ କୋଣ ରହିଥାଏ ଓ ଉତ୍ସ ଶ୍ରୋତା ଆଡ଼କୁ ସମଗତିରେ ଗତି କରୁଥାଏ, ତେବେ ପରିଲକ୍ଷିତ ଆବୃତ୍ତି ପ୍ରକୃତ ଆବୃତ୍ତିଠାରୁ ଅଧିକ ହୁଏ । କିନ୍ତୁ ଶ୍ରୋତା ପାଖରେ ପହଞ୍ଚିଲା ବେଳକୁ ଓ ତାହାଠାରୁ ଦୂରକୁ ଗଲାବେଳେ ଆବୃତ୍ତି କ୍ରମଶଃ କମ୍ ହୋଇଯାଏ । ଶ୍ରୋତା ଉତ୍ସର ଗତିପଥର ପାଖାପାଖି ଥିଲେ ତତ୍‍କ୍ଷଣାତ୍ ଉଚ୍ଚରୁ ନିମ୍ନ ଆବୃତ୍ତିର ଅନୁଭବ ହୁଏ । ଶ୍ରୋତା ଉତ୍ସର ଗତିପଥରୁ ଦୂରରେ ଥିଲେ ଏହି ପରିବର୍ତ୍ତନ ଧୀରେ ଧୀରେ ହେଲା ପରି ମନେ ହୁଏ ।

$v_{\text{s}}\,$ ଓ $v_{\text{r}}\,$ଙ୍କ ମାପ ତରଙ୍ଗର ବେଗଠାରୁ କମ୍ ହେଲେ, ପରିଲକ୍ଷିତ ଆବୃତ୍ତି $f$ ଓ ବିକିରିତ ଆବୃତ୍ତି $f_{\text{0}}$ ମଧ୍ୟରେ ରହିଥିବା ସମ୍ପର୍କକୁ ନିମ୍ନ ଭାବେ ଲେଖିହେବ

ପରିଲକ୍ଷିତ ଆବୃତ୍ତି	ଆବୃତ୍ତିରେ ପରିବର୍ତ୍ତନ
$f=\left(1+{\frac {\Delta v}{c}}\right)f_{0}$	$\Delta f={\frac {\Delta v}{c}}f_{0}$

ଏଠାରେ

$\Delta f=f-f_{0}\,$

$\Delta v=v_{\text{r}}-v_{\text{s}}\,$ ହେଉଛି ଶ୍ରୋତା ଓ ଉତ୍ସ ମଧ୍ୟରେ ରହିଥିବା ଆପେକ୍ଷିକ ବେଗ । ଉତ୍ସ ଓ ଶ୍ରୋତା ପରସ୍ପର ଆଡ଼କୁ ଗତି କରୁଥିଲେ ଏହାର ମାନ ଯୁକ୍ତମୁଖୀ ହୋଇଥାଏ ।

ପ୍ରମାଣ

$f=\left({\frac {c+v_{\text{r}}}{c+v_{\text{s}}}}\right)f_{0}\,$ ବନ୍ଧନୀ ମଧ୍ୟସ୍ଥ ଉଭୟ ଭାଜ୍ୟ ଓ ଭାଜକକୁ $c$ଦ୍ୱାରା ବିଭାଜିତ କଲେ $f=\left({\frac {1+{\frac {v_{\text{r}}}{c}}}{1+{\frac {v_{\text{s}}}{c}}}}\right)f_{0}=\left(1+{\frac {v_{\text{r}}}{c}}\right)\left({\frac {1}{1+{\frac {v_{\text{s}}}{c}}}}\right)f_{0}\,$

ଯେହେତୁ ${\frac {v_{\text{s}}}{c}}\ll 1$ ଏହି ଜ୍ୟାମିତିକ ସୂତ୍ରକୁ ପରିବର୍ତ୍ତିତ କରି ଆମେ ନିମ୍ନ ପ୍ରକାରରେ ଲେଖିପାରିବା : ${\frac {1}{1+{\frac {v_{\text{s}}}{c}}}}\approx 1-{\frac {v_{\text{s}}}{c}}$

ସ୍ଥିତାବସ୍ଥାରେ ରହିଥିବା ତରଙ୍ଗ ଉତ୍ସ f ଆବୃତ୍ତିର ତରଙ୍ଗ ସୃଷ୍ଟି କରୁଛି । ତରଙ୍ଗଗୁଡ଼ିକ ଉତ୍ସରୁ ସମମୀତ ଭାବେ c ବେଗରେ ଚାରିଆଡ଼କୁ ସଞ୍ଚାରିତ ହୁଅନ୍ତି । ପ୍ରତି ତରଙ୍ଗର ଦୁଇ ଶିଖର ବା ଗହ୍ୱର ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତାକୁ ତରଙ୍ଗଦୈର୍ଘ୍ୟ ବୋଲି କୁହାଯାଏ । ଏପରି ଦୃଷ୍ଟାନ୍ତରେ ସମସ୍ତ ଶ୍ରୋତା ବା ଦେଖଣାହାରୀଙ୍କ ପାଇଁ ପରିଲକ୍ଷିତ ଆବୃତ୍ତି ଓ ପ୍ରକୃତ ଆବୃତ୍ତି ସମାନ f = f0 ହେବ । ସ୍ଥିତାବସ୍ଥାରେ ରହିଥିବା ତରଙ୍ଗ ଉତ୍ସ f ଆବୃତ୍ତିର ତରଙ୍ଗ ସୃଷ୍ଟି କରୁଛି । ତରଙ୍ଗଗୁଡ଼ିକ ଉତ୍ସରୁ ସମମୀତ ଭାବେ c ବେଗରେ ଚାରିଆଡ଼କୁ ସଞ୍ଚାରିତ ହୁଅନ୍ତି । ପ୍ରତି ତରଙ୍ଗର ଦୁଇ ଶିଖର ବା ଗହ୍ୱର ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତାକୁ ତରଙ୍ଗଦୈର୍ଘ୍ୟ ବୋଲି କୁହାଯାଏ । ଏପରି ଦୃଷ୍ଟାନ୍ତରେ ସମସ୍ତ ଶ୍ରୋତା ବା ଦେଖଣାହାରୀଙ୍କ ପାଇଁ ପରିଲକ୍ଷିତ ଆବୃତ୍ତି ଓ ପ୍ରକୃତ ଆବୃତ୍ତି ସମାନ f = f0 ହେବ ।  ଏହି ଚିତ୍ରରେ ସେହି ଉତ୍ସଟି ସମାବୃତ୍ତିରେ ତରଙ୍ଗ ସୃଷ୍ଟି କରୁଛି କିନ୍ତୁ ଉତ୍ସଟି υ0= 0.7 c ବେଗରେ ଗତି କରୁଛି । ଉତ୍ସର ବେଗ ତରଙ୍ଗର ବେଗର ପ୍ରାୟ ୭୦% । ଉତ୍ସଟି ଗତିଶୀଳ ଥିବାରୁ ପ୍ରତ୍ୟେକ ତରଙ୍ଗର ଆରମ୍ଭ ବିନ୍ଦୁ ଡାହାଣ ପଟକୁ ସାମାନ୍ୟ ବିସ୍ଥାପିତ ହୋଇଛି । ଏହା ଫଳରେ ତରଙ୍ଗର ଆରମ୍ଭ ବିନ୍ଦୁଗୁଡ଼ିକ ଡାହାଣ ପଟେ ଏକତ୍ରିତ ଓ ବାମ ପଟେ ଦୂରେଇ ଯାଇଛନ୍ତି । ଡାହାଣ ପଟେ ରହିଥିବା ଏକ ଶ୍ରୋତା ପରିବର୍ଦ୍ଧିତ ଆବୃତ୍ତି ଓ ବାମପଟେ ରହିଥିବା ଶ୍ରୋତା ନିମ୍ନ ଆବୃତ୍ତି ଶୁଣିବାକୁ ପାଇବ । ଡାହାଣ ପଟେ ରହିଥିବା ଶ୍ରୋତା ପାଇଁ f = c + 0/c - 0.7c f0 = 3.33 f0 ବାମ ପଟେ ରହିଥିବା ଶ୍ରୋତା ପାଇଁ f = c - 0/c + 0.7c f0 = 0.59 f0 ଏହି ଚିତ୍ରରେ ସେହି ଉତ୍ସଟି ସମାବୃତ୍ତିରେ ତରଙ୍ଗ ସୃଷ୍ଟି କରୁଛି କିନ୍ତୁ ଉତ୍ସଟି υ0= 0.7 c ବେଗରେ ଗତି କରୁଛି । ଉତ୍ସର ବେଗ ତରଙ୍ଗର ବେଗର ପ୍ରାୟ ୭୦% । ଉତ୍ସଟି ଗତିଶୀଳ ଥିବାରୁ ପ୍ରତ୍ୟେକ ତରଙ୍ଗର ଆରମ୍ଭ ବିନ୍ଦୁ ଡାହାଣ ପଟକୁ ସାମାନ୍ୟ ବିସ୍ଥାପିତ ହୋଇଛି । ଏହା ଫଳରେ ତରଙ୍ଗର ଆରମ୍ଭ ବିନ୍ଦୁଗୁଡ଼ିକ ଡାହାଣ ପଟେ ଏକତ୍ରିତ ଓ ବାମ ପଟେ ଦୂରେଇ ଯାଇଛନ୍ତି । ଡାହାଣ ପଟେ ରହିଥିବା ଏକ ଶ୍ରୋତା ପରିବର୍ଦ୍ଧିତ ଆବୃତ୍ତି ଓ ବାମପଟେ ରହିଥିବା ଶ୍ରୋତା ନିମ୍ନ ଆବୃତ୍ତି ଶୁଣିବାକୁ ପାଇବ । ଡାହାଣ ପଟେ ରହିଥିବା ଶ୍ରୋତା ପାଇଁ f = c + 0/c - 0.7c f0 = 3.33 f0 ବାମ ପଟେ ରହିଥିବା ଶ୍ରୋତା ପାଇଁ f = c - 0/c + 0.7c f0 = 0.59 f0   ଏହି ଉଦାହରଣରେ ଉତ୍ସର ବେଗ υ0= c ତରଙ୍ଗର ବେଗ ସହିତ ସମାନ । ଏପରି ଅବସ୍ଥା ସୃଷ୍ଟି ହୋଇଥିବାରୁ ସମସ୍ତ ତରଙ୍ଗ ଆରମ୍ଭ ବିନ୍ଦୁ ଗୋଟିଏ ବିନ୍ଦୁରେ ଏକତ୍ରିତ ହୋଇଯାଇଛନ୍ତି । ଯେତେବେଳ ଯାଏଁ ତରଙ୍ଗଟି ଡାହାଣ ପଟେ ରହିଥିବା ଶ୍ରୋତା ନିକଟରେ ନ ପହଞ୍ଚିଛି ସେ ଏହି ଶବ୍ଦକୁ ଶୁଣି ପାରିବ ନାହିଁ । f = c + 0/c - c f0 = ∞ ବାମ ପଟେ ରହିଥିବା ଶ୍ରୋତା ପାଇଁ f = c - 0/c + c f0 = 0.5 f0 ଏହି ଉଦାହରଣରେ ଉତ୍ସର ବେଗ υ0= c ତରଙ୍ଗର ବେଗ ସହିତ ସମାନ । ଏପରି ଅବସ୍ଥା ସୃଷ୍ଟି ହୋଇଥିବାରୁ ସମସ୍ତ ତରଙ୍ଗ ଆରମ୍ଭ ବିନ୍ଦୁ ଗୋଟିଏ ବିନ୍ଦୁରେ ଏକତ୍ରିତ ହୋଇଯାଇଛନ୍ତି । ଯେତେବେଳ ଯାଏଁ ତରଙ୍ଗଟି ଡାହାଣ ପଟେ ରହିଥିବା ଶ୍ରୋତା ନିକଟରେ ନ ପହଞ୍ଚିଛି ସେ ଏହି ଶବ୍ଦକୁ ଶୁଣି ପାରିବ ନାହିଁ । f = c + 0/c - c f0 = ∞ ବାମ ପଟେ ରହିଥିବା ଶ୍ରୋତା ପାଇଁ f = c - 0/c + c f0 = 0.5 f0   ଏହି ଉଦାହରଣରେ ଉତ୍ସର ବେଗ ତରଙ୍ଗର ବେଗଠାରୁ ପ୍ରାୟ ୪୦% ଅଧିକ । ଉତ୍ସଟି ତରଙ୍ଗଠାରୁ ଅଧିକ ବେଗରେ ଗତି କରୁଥିବାରୁ ଡାହାଣ ପଟେ ରହିଥିବା ଏକ ଶ୍ରୋତା ତାକୁ ଉତ୍ସ ପାର କରି କିଛି ଦୂର ଅଗ୍ରସର ହେବା ପରେ ଧ୍ୱନି ଶୁଣିବାକୁ ମିଳିବ । ତେଣୁ ଡାହାଣ ପଟେ ରହିଥିବା ଶ୍ରୋତା ପାଇଁ f = c + 0/c - 1.4c f0= -2.5 f0 ଓ ବାମ ପଟେ ରହିଥିବା ଶ୍ରୋତା ପାଇଁ f = c - 0/c + 1.4c f0 = 0.42 f0 ବାୟୁସେନାର ଶୁଖୋଇ ଜେଟ୍ ଆକାଶରେ ଉଡ଼ିଗଲେ ଆମକୁ ଏପରି ପ୍ରଭାବ ସ୍ପଷ୍ଟ ଭାବେ ଜଣାପଡ଼େ । ଏହି ଉଦାହରଣରେ ଉତ୍ସର ବେଗ ତରଙ୍ଗର ବେଗଠାରୁ ପ୍ରାୟ ୪୦% ଅଧିକ । ଉତ୍ସଟି ତରଙ୍ଗଠାରୁ ଅଧିକ ବେଗରେ ଗତି କରୁଥିବାରୁ ଡାହାଣ ପଟେ ରହିଥିବା ଏକ ଶ୍ରୋତା ତାକୁ ଉତ୍ସ ପାର କରି କିଛି ଦୂର ଅଗ୍ରସର ହେବା ପରେ ଧ୍ୱନି ଶୁଣିବାକୁ ମିଳିବ । ତେଣୁ ଡାହାଣ ପଟେ ରହିଥିବା ଶ୍ରୋତା ପାଇଁ f = c + 0/c - 1.4c f0= -2.5 f0 ଓ ବାମ ପଟେ ରହିଥିବା ଶ୍ରୋତା ପାଇଁ f = c - 0/c + 1.4c f0 = 0.42 f0 ବାୟୁସେନାର ଶୁଖୋଇ ଜେଟ୍ ଆକାଶରେ ଉଡ଼ିଗଲେ ଆମକୁ ଏପରି ପ୍ରଭାବ ସ୍ପଷ୍ଟ ଭାବେ ଜଣାପଡ଼େ ।

ବିଶ୍ଳେଷଣ

ସରଳ ଭାବେ ବୁଝିବା ପାଇଁ ଆଉ ଏକ ତୁଳନାତ୍ମକ ଉଦାହରଣ ପ୍ରଦତ୍ତ ହେଲା । ମନେ କରାଯାଉ ଗୋଟିଏ ଯନ୍ତ୍ରରୁ ଜଣେ ବ୍ୟକ୍ତିଙ୍କ ଆଡ଼କୁ ପ୍ରତି ସେକେଣ୍ଡରେ ଗୋଟିଏ ବଲ୍ ଫିଙ୍ଗା ଯାଉଛି । ଫିଙ୍ଗା ଯାଉଥିବା ବଲ୍‍ର ବେଗ ସର୍ବଦା ସମାନ । ଯଦି ଯନ୍ତ୍ରଟି ସ୍ଥିରାବସ୍ଥାରେ ଥାଏ ତେବେ ବ୍ୟକ୍ତିଙ୍କୁ ପ୍ରତି ସେକେଣ୍ଡରେ ଗୋଟିଏ ବଲ୍ ମିଳିବ । କିନ୍ତୁ ଯଦି ଯନ୍ତ୍ରଟି ବ୍ୟକ୍ତିଙ୍କ ଆଡ଼କୁ ଗତି କରେ ତେବେ ବ୍ୟକ୍ତି ଜଣକ ଏକ ସେକେଣ୍ଡ ହେବା ପୂର୍ବରୁ ପରବର୍ତ୍ତୀ ବଲ୍‍ଟି ପାଇବେ । ଯନ୍ତ୍ରଟି ପୁରା ପାଖକୁ ଆସିବା ବେଳକୁ ଶୀଘ୍ର ଶୀଘ୍ର ବଲ୍ ମିଳିବ । ସେହିପରି ଯନ୍ତ୍ରଟି ଦୂରକୁ ଗଲେ ବିଳମ୍ବରେ ବଲ୍ ମିଳିବ । ତରଙ୍ଗ ଦୃଷ୍ଟିକୋଣରୁ ଦେଖାଗଲେ ଏହାର ବେଗ ସମାନ ଥାଇ ତରଙ୍ଗ ଦୈର୍ଘ୍ୟ ପ୍ରଭାବିତ ହେବା ଯୋଗୁଁ ଏହାର ଆବୃତ୍ତି ମଧ୍ୟ ପ୍ରଭାବିତ ହୁଏ । ମାଧ୍ୟମରେ ଶ୍ରୋତା ସ୍ଥିର ହୋଇ ରହିଥିଲେ ଓ ଉତ୍ସ $f_{\text{0}}$ ଆବୃତ୍ତିର ତରଙ୍ଗ ବିକିରଣ କରି ଗତି କରୁଥିଲେ, କେବଳ ତରଙ୍ଗ ଦୈର୍ଘ୍ୟ ବଦଳେ, ସଞ୍ଚାରିତ ତରଙ୍ଗର ବେଗ ଏକ ସ୍ଥିରାଙ୍କ ${\text{--}}$ ଓ ତରଙ୍ଗର ବେଗ ଓ ଉତ୍ସର ବେଗ ମଧ୍ୟରେ କୌଣସି ସମ୍ପର୍କ ନାହିଁ । ଏପରି ସ୍ଥିତିରେ ଶ୍ରୋତାଦ୍ୱାରା ପରିଲକ୍ଷିତ ଆବୃତ୍ତି $f$ର ସୂତ୍ର ହେଉଛି

$f=\left({\frac {c}{c+v_{\text{s}}}}\right)f_{0}$

ସେହିପରି ଉତ୍ସ ସ୍ଥିର ଥାଇ ଶ୍ରୋତା ଗତିଶୀଳ ଥିଲେ, ତରଙ୍ଗ ଦୈର୍ଘ୍ୟ ଅପରିବର୍ତ୍ତିତ ରହେ । କିନ୍ତୁ ଶ୍ରୋତା ପାଖରେ ପହଞ୍ଚୁଥିବା ତରଙ୍ଗର ହାର ${\text{--}}$ ବଦଳେ ଓ ତରଙ୍ଗର ସଞ୍ଚାରଣ ବେଗ ଯୋଗୁଁ ଆବୃତ୍ତିରେ ପରିବର୍ତ୍ତନ ଦେଖାଦିଏ । ଏପରି ଅବସ୍ଥାରେ ପରିଲକ୍ଷିତ ଆବୃତ୍ତିର ସୂତ୍ର ହେଉଛି

$f=\left({\frac {c+v_{\text{r}}}{c}}\right)f_{0}$

ଏହାକୁ ଏକ ପୂର୍ଣ୍ଣାଙ୍ଗ ସମୀକରଣ ରୂପରେ ଲେଖିଲେ

$f=\left({\frac {c+v_{\text{r}}}{c+v_{\text{s}}}}\right)f_{0}$

ଲର୍ଡ୍ ରେଲେ ନିଜ ଶବ୍ଦ ସମ୍ବନ୍ଧୀୟ ପୁସ୍ତକରେ ଏହାକୁ ନେଇ ଏକ ମଜା ତଥ୍ୟ କହିଥିଲେ । ତାଙ୍କ ଅନୁସାରେ ଯଦି ଶ୍ରୋତା ଆଡ଼କୁ ଗତିଶୀଳ ଉତ୍ସର ବେଗ ଶବ୍ଦର ବେଗର ଦୁଇ ଗୁଣ ହୁଏ ଓ ଉତ୍ସରେ ସା-ରେ-ଗା ଧ୍ୱନି ବାଜେ, ତେବେ ଶ୍ରୋତା ସବୁ ଧ୍ୱନି ଶୁଣିବ କିନ୍ତୁ ସା-ରେ-ଗା ବଦଳରେ ତାକୁ ଏହା ଗା-ରେ-ସା ଶୁଭାଯିବ । ଶବ୍ଦ ତରଙ୍ଗରେ ଡୋପ୍ଲର୍ ପ୍ରଭାବ ଖୁବ୍ ସ୍ପଷ୍ଟଭାବେ ପରିଲକ୍ଷିତ ହୁଏ । କୌଣସି ଗତିଶୀଳ ବସ୍ତୁରେ ଏକ ଅଲ୍‍ଟ୍ରାସୋନିକ୍ ଏମିଟର୍ ଖଞ୍ଜି ଦେଲେ କିପରି ଡୋପ୍ଲର୍ ପ୍ରଭାବ ସହଜରେ ଅନୁଭବ କରାଯାଇପାରିବ ତାହା ନୀଲ୍ ଏ. ଡୌନି ପରୀକ୍ଷାଦ୍ୱାରା ପ୍ରଦର୍ଶିତ କରିଥିଲେ ।

ବ୍ୟବହାର

ସାଇରନ୍

ଦମକଳ ବା ଆମ୍ବୁଲାଂସ୍ ପରି ଜରୁରୀକାଳୀନ ସେବା ପାଇଁ ଉଦ୍ଦିଷ୍ଟ ଗାଡ଼ି ପାଖକୁ ଆସିବା ବେଳେ ତାର ସାଇରନ୍‍ର ତୀବ୍ରତା ବଢ଼ିଲା ପରି ଲାଗେ, ତା’ପରେ ସାଇରନ୍ ଶ୍ରୋତାକୁ ପାର କରିଗଲା ପରେ ତାହା ଧୀରେ ଧୀରେ କମେ ।

ମହାକାଶ ବିଜ୍ଞାନ

ସୂର୍ଯ୍ୟରୁ ଆସୁଥିବା ଆଲୋକର ବିଚ୍ଛୁରଣକୁ ଭିତ୍ତି କରି ଅତି ଦୂରର ଆକାଶଗଙ୍ଗାରୁ ଆସୁଥିବା ଆଲୋକର ବିଚ୍ଛୁରଣ ଯୋଗୁଁ ହେଉଥିବା ଲୋହିତ ବିସ୍ଥାପନ ଡୋପ୍ଲର୍ ପ୍ରଭାବର ଏକ ଉଦାହରଣ

ଆମ ଗ୍ରହ ଆଡ଼କୁ ଆସୁଥିବା ତାରକାର ଆଲୋକ ନୀଳ ବିସ୍ଥାପିତ ଓ ଆମଠାରୁ ଦୂରକୁ ଯାଉଥିବା ତାରକାର ଆଲୋକ ଲୋହିତ ବିସ୍ଥାପିତ ହୋଇଥାଏ

ଆଲୋକ ପରି ବିଦ୍ୟୁତ୍-ଚୁମ୍ବକୀୟ ତରଙ୍ଗରେ ଡୋପ୍ଲର୍ ପ୍ରଭାବ ଯୋଗୁଁ ନୀଳ ବିସ୍ଥାପନ ବା ଲୋହିତ ବିସ୍ଥାପନ ଦେଖାଦିଏ ଓ ଏହି ବିସ୍ଥାପନକୁ ଆଧାର କରି ମହାକାଶ ବିଜ୍ଞାନୀମାନେ ଅନେକ ପରୀକ୍ଷଣ କରିଥାନ୍ତି । ନୀଳ ଓ ଲୋହିତ ବିସ୍ଥାପନର ଅନୁଧ୍ୟାନ କରି ଅନ୍ୟ ଏକ ତାରକା ବା ଆକାଶ ଗଙ୍ଗା ଆମ ଆଡ଼କୁ କେତେ ବେଗରେ ଆସୁଛି ବା ଆମଠାରୁ କେତେ ବେଗରେ ଦୂରକୁ ଯାଉଛି ତାହା ଜାଣିହେବ । ଏହି ବିସ୍ଥାପନର ମାତ୍ରା ଅତି କମ୍ ଥାଏ ।

ଆଉ ଏକ ଜାଣିବା ବିଷୟ ହେଲା ଯେ ଲୋହିତ ବିସ୍ଥାପନଦ୍ୱାରା ଆମ ମହାକାଶ କେତେ ପ୍ରସାରିତ ହୋଇଛି ତାହା ମଧ୍ୟ ସ୍ଥିର କରାଯାଏ । କିନ୍ତୁ ଏପ୍ରକାରର ଲୋହିତ ବିସ୍ଥାପନ ଡୋପ୍ଲର୍ ପ୍ରଭାବ ଯୋଗୁଁ ସୃଷ୍ଟି ହୋଇନଥାଏ । ବରଂ ଏହି ପ୍ରକାରର ଲୋହିତ ବିସ୍ଥାପନକୁ ମହାକାଶୀୟ ଲୋହିତ ବିସ୍ଥାପନ କୁହାଯାଏ ଓ ସାଧାରଣ ଆପେକ୍ଷିକ ତତ୍ତ୍ୱ ବା ରବର୍ଟସନ୍-ୱାକର୍ ମାପକଦ୍ୱାରା ଏହି ବିସ୍ଥାପନ ନିର୍ଦ୍ଧାରିତ ହୁଏ ।

ରେଡ଼ାର୍ ବା ରାଡ଼ାର୍

ଡୋପ୍ଲର୍ ପ୍ରଭାବକୁ ବ୍ୟବହାର କରି ଡୋପ୍ଲର୍ ରେଡାର୍‍ ନାମକ ଏକ ରେଡାର୍ ନିର୍ମିତ ହୋଇଛି । ରେଡାର୍‍ର କ୍ଷେତ୍ର ମଧ୍ୟରେ ଉଡ଼ୁଥିବା କୌଣସି ବସ୍ତୁ ଆଡ଼କୁ ରେଡାର୍‍ରୁ ଏକ ରଶ୍ମୀ ଛଡ଼ାଯାଏ । କ୍ରମାଗତ ଛଡ଼ାଯାଇଥିବା ଦୁଇଟି ରଶ୍ମୀ କେତେ ସମୟ ବ୍ୟବଧାନରେ ବସ୍ତୁ ନିକଟରୁ ପ୍ରତିଫଳିତ ହେଉଛନ୍ତି ତାହା ଅନୁଧ୍ୟାନ କରାଯାଏ । ବସ୍ତୁଟି ପାଖକୁ ଆସିବା ବେଳେ ଓ ଅତିକ୍ରମ କରି ଦୂରକୁ ଯିବା ବେଳେ ମଧ୍ୟ ଏହି ଦୁଇଟି ରଶ୍ମୀ ରେଡାର୍‍ରୁ ଛଡ଼ାଯାଇପାରିବ । ଯେକୌଣସି ଉପାୟ ଅବଲମ୍ବନ କଲେ ମଧ୍ୟ ଡୋପ୍ଲର୍ ପ୍ରଭାବଦ୍ୱାରା ବସ୍ତୁର ବେଗ ଜାଣିହେବ । ଟ୍ରାଫିକ୍ ସ୍ପିଡ୍‍ଗନ୍ ଏହି ପଦ୍ଧତିର ବ୍ୟବହାର କରି ମୋଟର ଗାଡ଼ିର ବେଗ ନିର୍ଣ୍ଣୟ କରନ୍ତି ଓ ନିର୍ଦ୍ଧାରିତ ସୀମାରୁ ଅଧିକ ବେଗରେ ଗାଡ଼ି ଯାଉଥିଲେ ଗାଡ଼ି ଓ ଚାଳକର ଚିତ୍ର ଉତ୍ତୋଳନ କରି ରଖାଯାଏ । ଦ୍ୱିତୀୟ ବିଶ୍ୱଯୁଦ୍ଧ ସମୟରେ ନିର୍ମିତ ପ୍ରକ୍ସିମିଟି ଫ୍ୟୁଜ୍ ମଧ୍ୟ ଡପ୍ଲର୍ ପ୍ରଭାବର ବ୍ୟବହାର କରେ ।

ସ୍ଥିର ରେଡାର୍ ଓ ଗତିଶୀଳ ମୋଟର କାରର ଆପେକ୍ଷିକ ବେଗ $\Delta v$ ଦ୍ୱିଗୁଣିତ ହୋଇଯାଉଥିବାରୁ ମୋଟର ଗାଡ଼ିକୁ ବାଜିଥିବା ରଶ୍ମୀ ଓ ସେଥିରୁ ପ୍ରତିଫଳିତ ରଶ୍ମୀର ଆବୃତ୍ତିରେ ଦେଖାଯାଉଥିବା ପରିବର୍ତ୍ତନ ହେଲା :

$\Delta f={\frac {2\Delta v}{c}}f_{0}$

ଚିକିତ୍ସା

ଡୋପ୍ଲର୍ ପ୍ରଭାବର ବ୍ୟବହାର କରି ହେଉଥିବା ଅଲ୍‍ଟ୍ରା-ସୋନେଗ୍ରାଫି

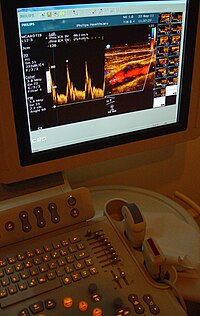
ଡୋପ୍ଲର୍ ପ୍ରଭାବର ସିଦ୍ଧାନ୍ତ ଉପରେ ଆଧାରିତ ଇକୋ-କାର୍ଡିଓଗ୍ରାମ୍ ଯନ୍ତ୍ରଦ୍ୱାରା ରକ୍ତ ପ୍ରବାହର ଦିଗ, ରକ୍ତର ବେଗ ମାପିବା ତଥା ହୃତ୍‍ପିଣ୍ଡ ସମ୍ବନ୍ଧୀୟ କୋଷର ଅବସ୍ଥିତି ନିର୍ଦ୍ଧାରଣ କରାଯାଇଥାଏ । ଅଲ୍‍ଟ୍ରାସାଉଣ୍ଡ ରଶ୍ମୀ ରକ୍ତ ପ୍ରବାହ ସହିତ ସମାନ୍ତରାଳ ଭାବେ ଗତି କରିବା ଆବଶ୍ୟକ ହୋଇଥାଏ । ବେଗର ମାପରୁ ହୃତ୍‍ପିଣ୍ଡ କିପରି କାର୍ଯ୍ୟ କରୁଛି, ହୃତ୍‍ପିଣ୍ଡର ବାମ ପାର୍ଶ୍ୱ ଓ ଦକ୍ଷିଣ ପାର୍ଶ୍ୱ ସଠିକ୍ ଭାବେ ଚଳପ୍ରଚଳ ହେଉଛି ନା ନାହିଁ, ଭାଲ୍‍ଭ୍ ଦ୍ୱାରରୁ ରକ୍ତ କ୍ଷରଣ ହେଉଛି କି ଇତ୍ୟାଦି ଜାଣି ହେବ । କ୍ଷୁଦ୍ର ଗ୍ୟାସୀୟ ଫୋଟକା ରହିଥିବା କଣ୍ଟ୍ରାଷ୍ଟ୍ ଏନ୍‍ହାଂସ୍‍ଡ୍ ଅଲ୍‍ଟ୍ରାସାଉଣ୍ଡ ବ୍ୟବହାର କଲେ ବେଗର ମାପ ଅଧିକ ସଠିକ ଭାବେ କରାଯାଇପାରିବ । ବେଗର ମାପ ପାଇଁ ଡୋପ୍ଲର୍ ପ୍ରଭାବ ବ୍ୟବହାର ହୁଏ ସତ, କିନ୍ତୁ ଆବୃତ୍ତି ବିସ୍ଥାପନ ପରିବର୍ତ୍ତେ ଏହି ଯନ୍ତ୍ରରେ କଳା ବିସ୍ଥାପନ (Phase Shift)ରୁ ଡୋପ୍ଲର୍ ପ୍ରଭାବ ସମ୍ପର୍କୀୟ ଗଣନା କରାଯାଇଥାଏ । ଓବ୍‍ଷ୍ଟେରିକ୍ ଅଲ୍‍ଟ୍ରାସୋନୋଗ୍ରାଫି, ନ୍ୟୁରୋଲୋଜି ପରି ଅନେକ କ୍ଷେତ୍ରରେ ଅଲ୍‍ଟ୍ରାସୋନୋଗ୍ରାଫିଦ୍ୱାରା ରକ୍ତ ପ୍ରବାହର ବେଗ ନିରୂପଣ କରାଯାଇଥାଏ । ଷ୍ଟେନୋସିସ୍ ପରି ଅବସ୍ଥାର ନିରାକରଣ ପାଇଁ ଶିରା ଓ ଧମନୀରେ ରକ୍ତ ପ୍ରବାହର ବେଗ ନିରୂପଣ କରିବା ଅତି ଜରୁରୀ ଏବଂ ଏଥିପାଇଁ ଡୋପ୍ଲର୍ ପ୍ରଭାବକୁ ଆଧାର କରି ଚିକିତ୍ସା ଉପକରଣମାନ ନିର୍ମିତ ହୋଇଥାଏ ।

ପ୍ରବାହର ମାପ

ତରଳ ପଦାର୍ଥର ପ୍ରବାହ ମାପିବା ପାଇଁ ଲେଜର୍ ଡୋପ୍ଲର୍ ଭେଲୋସିମିଟର୍ (Laser Doppler Velocimeter - LDV), ଅକୋଷ୍ଟିକ୍ ଡୋପ୍ଲର୍ ଭେଲୋସିମିଟର୍ (Acoustic Doppler Velocimeter - ADV) ଆଦି ଉପକରଣ ବ୍ୟବହୃତ ହୁଏ । LDVରେ ଆଲୋକ ରଶ୍ମୀ ଓ ADVରେ ଶବ୍ଦ ତରଙ୍ଗ ପ୍ରେରଣ କରି ଡୋପ୍ଲର୍ ପ୍ରଭାବ ଯୋଗୁଁ ହେଉଥିବା ପ୍ରତିଫଳନ ଓ ପ୍ରାରମ୍ଭିକ ତରଙ୍ଗର ଦୈର୍ଘ୍ୟରେ ପରିବର୍ତ୍ତନ ମପାଯାଏ । ତରଳ ପଦାର୍ଥର ପ୍ରବାହ ତାହାର ବେଗ ଓ କଳା (Phase)ର ଫଳନ ।

ବିପରୀତ ଡୋପ୍ଲର୍ ପ୍ରଭାବ

୧୯୬୮ ମସିହାରୁ ଭିକ୍ଟର୍ ୱେସେଲାଗୋ ଓ ଅନ୍ୟ କେତେକ ବୈଜ୍ଞାନିକ ଏକ ବିପରୀତ ଡୋପ୍ଲର୍ ପ୍ରଭାବ ସମ୍ଭାବନା ବିଷୟରେ କହି ଆସୁଛନ୍ତି । ୨୦୦୩ ମସିହାରେ ଯୁକ୍ତରାଜ୍ୟର ବ୍ରିଷ୍ଟଲ୍ ସହରରେ ନାଇଜେଲ୍ ସେଡ୍ଡୋନ୍ ଓ ଟ୍ରେଭର୍ ବେର୍ପାର୍କଙ୍କଦ୍ୱାରା କରାଯାଇଥିବା ପରୀକ୍ଷଣ ଏହି ବିପରୀତ ପ୍ରଭାବ ରହିଥିବାର ଦାବୀକୁ ଖୋରାକ ଯୋଗାଇଛି ।

ଆହୁରି ଦେଖନ୍ତୁ

ଆପେକ୍ଷିକ ଡୋପ୍ଲର୍ ପ୍ରଭାବ

ଡୋପ୍ଲର୍ ଶୀତଳୀକରଣ