ବିଦ୍ୟୁତ୍ ବିଭବ
| ବିଦ୍ୟୁତ୍ - ଚୁମ୍ବକୀୟତା |
|---|
 |
ଗୋଟିଏ ବୈଦୁତିକ କ୍ଷେତ୍ର ଏକ ଧନାତ୍ମକ ଚାର୍ଜକୁ ଅନନ୍ତ ଦୂରତାରୁ ସେହି ବିନ୍ଦୁ ପର୍ଯ୍ୟନ୍ତ ଆଣିବା ପାଇଁ ଯେତିକି କାର୍ଯ୍ୟ କରିଥାଏ, ତା'କୁ ବିଦ୍ୟୁତ୍ ବିଭବ ବା ଇଲେକ୍ଟ୍ରିକ୍ ପୋଟେନ୍ସିଆଲ୍ କୁହାଯାଏ ।
ସ୍ଥିର ବିଦ୍ୟୁତ
[ସମ୍ପାଦନା]ଯଦି ଏକ ସ୍ଥିର ବୈଦୁତିକ କ୍ଷେତ୍ର Eଠାରେ r ଏକ ବିନ୍ଦୁ ହୁଏ, ତେବେ ସେହି ବିନ୍ଦୁରେ 'ବିଦ୍ୟୁତ୍ ବିଭବ' ଏହାର ଲାଇନ୍ ଇଣ୍ଟିଗ୍ରାଲ୍ଦ୍ୱାରା ନିର୍ଣ୍ଣୟ କରାଯିବ –
ଏଠାରେ C ହେଉଛି ଏକ ଅନିର୍ଦ୍ଧିଷ୍ଟ ପଥ (arbitrary path), ଯାହାକି 'ଜିରୋ ବିଭବ' (zero potential)ରେ ଥିବା ଏକ ବିନ୍ଦୁକୁ r ସହ ଯୋଗ କରେ । ଯେତେବେଳେ କର୍ଲ୍ (curl) ∇ × E ଶୁନ ହୁଏ, ଉପରୋକ୍ତ line integral ଆଉ C ପଥ ଉପରେ ନିର୍ଭରଶୀଳ ହୋଇ ନରହି କେବଳ ଅନ୍ତିମ-ବିନ୍ଦୁ ଗୁଡ଼ିକ (endpoints) ଉପରେ ନିର୍ଭର କରେ । ଏହି ପରିପ୍ରେକ୍ଷୀରେ, ବୈଦୁତିକ-କ୍ଷେତ୍ରଟି ବିଭବ(ପୋଟେନ୍ସିଆଲ୍)ର ଗ୍ରାଡ଼ିଏଣ୍ଟ (gradient) ଉପରେ ନିର୍ଭର କରେ:
ତା'ହେଲେ ବର୍ତ୍ତମାନ, ଗସ୍ଙ୍କ ନିୟମ ଅନୁସାରେ, ପୋଟେନ୍ସିଆଲ୍ ପଏଜନ୍ଙ୍କ ସମୀକରଣକୁ satisfy କରୁଛି:
ଏଠାରେ ρ ହେଉଛି total charge density ଏବଂ ∇· ଡାଇଭର୍ଜେନ୍ସ (divergence)କୁ ସୁଚାଏ ।
ପଏଣ୍ଟ ଚାର୍ଜ ଯୋଗୁଁ ସୃଷ୍ଟ ବିଦ୍ୟୁତ ବିଭବ
[ସମ୍ପାଦନା]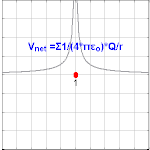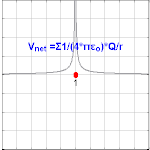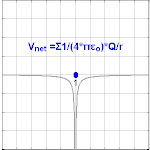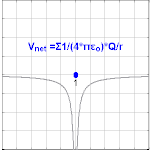
ଚାର୍ଜଠାରୁ r ଦୁରତ୍ୱରେ, ଗୋଟିଏ ପଏଣ୍ଟ ଚାର୍ଜ Q ଯୋଗୁଁ ସୃଷ୍ଟ ବିଦ୍ୟୁତ ବିଭବକୁ ଆମେ ଲେଖିପାରିବା ଯେ:
ଏଠାରେ ε0 ହେଉଛି ଏକ ବୈଦୁତିକ ସ୍ଥିରାଙ୍କ (permittivity of vacuum) । ଏହାକୁ 'କୁଲମ୍ବଙ୍କ ବିଭବ' (Coulomb potential) କୁହାଯାଏ ।
ଚଳ ବିଦ୍ୟୁତ
[ସମ୍ପାଦନା]ଏକକ
[ସମ୍ପାଦନା]ଆହୁରି ଦେଖନ୍ତୁ
[ସମ୍ପାଦନା]ଆଧାର
[ସମ୍ପାଦନା]- Griffiths, David J. (1998). Introduction to Electrodynamics (3rd. ed.). Prentice Hall. ISBN 0-13-805326-X.
- Jackson, John David (1999). Classical Electrodynamics (3rd. ed.). USA: John Wiley & Sons, Inc. ISBN 978-0-471-30932-1.
- Wangsness, Roald K. (1986). Electromagnetic Fields (2nd., Revised, illustrated ed.). Wiley. ISBN 978-0-471-81186-2.




