ଜର୍ଜ କ୍ୟାଣ୍ଟର
ଉଇକିପିଡ଼ିଆ ରୁ
| ଜର୍ଜ କ୍ୟାଣ୍ଟର | |
|---|---|
 |
|
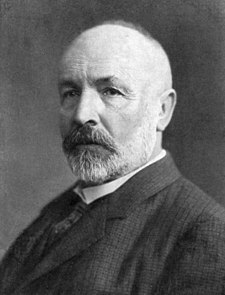| ଜନ୍ମ | ଜର୍ଜ ଫର୍ଡିନାଣ୍ଡ ଲୁଡୱିଗ ଫିଲିପ କ୍ୟାଣ୍ଟର ମାର୍ଚ ୩, ୧୮୪୫ ସେଣ୍ଟ ପିଟସବର୍ଗ |
| ମୃତ୍ୟୁ | ୬ ଜାନୁଆରି, ୧୯୧୮ (୭୨ ବର୍ଷ) ହାଲେ |
| ଜାତୀୟତା | ଜର୍ମାନ |
ବିଖ୍ୟାତ ଜର୍ମାନ ବୈଜ୍ଞାନିକ । ସେଟ୍ ତତ୍ଵର ଉଦ୍ଭାବକ ଭାବେ ପ୍ରସିଦ୍ଧ ।
ଆଧାର [ସମ୍ପାଦନା]
ଅଧିକ ଦେଖନ୍ତୁ [ସମ୍ପାଦନା]
- Older sources on Cantor's life should be treated with caution. See Historiography section above.
- Primary literature in English
- Cantor, Georg (1955), written at New York, Philip Jourdain, ed., Contributions to the Founding of the Theory of Transfinite Numbers, Dover, ISBN 978-0-486-60045-1, http://www.archive.org/details/contributionstot003626mbp.
- Ewald, William B., ed. (1996), written at New York, From Immanuel Kant to David Hilbert: A Source Book in the Foundations of Mathematics, Oxford University Press, ISBN 978-0-19-853271-2.
- Primary literature in German
- Cantor, Georg (1874), "Über eine Eigenschaft des Ingebriffes aller reelen algebraischen Zahlen", Journal für die Reine und Angewandte Mathematik 77, http://bolyai.cs.elte.hu/~badam/matbsc/11o/cantor1874.pdf.
- Cantor, Georg (1932), Ernst Zermelo, ed., Gesammelte Abhandlungen mathematischen und philosophischen inhalts, http://philosophons.free.fr/philosophes/cantor1932.pdf. Almost everything that Cantor wrote.
- Hilbert, David (1926), "Über das Unendliche", Mathematische Annalen 95, doi:10.1007/BF01206605, http://www.digizeitschriften.de/main/dms/img/?PPN=GDZPPN002270641.
- Secondary literature
- Aczel, Amir D. (2000), written at New York, The mystery of the Aleph: Mathematics, the Kabbala, and the Human Mind, Four Walls Eight Windows Publishing. ISBN 0-7607-7778-0. A popular treatment of infinity, in which Cantor is frequently mentioned.
- Dauben, Joseph W. (1977), "Georg Cantor and Pope Leo XIII: Mathematics, Theology, and the Infinite", Journal of the History of Ideas 38 (1).
- Dauben, Joseph W. (1979), written at Boston, Georg Cantor: his mathematics and philosophy of the infinite, Harvard University Press. The definitive biography to date. ISBN 978-0-691-02447-9
- Dauben, Joseph W. (1983), "Georg Cantor and the Origins of Transfinite Set Theory", Scientific American 248 (6)
- Dauben, Joseph (1993, 2004), "Georg Cantor and the Battle for Transfinite Set Theory", Proceedings of the 9th ACMS Conference (Westmont College, Santa Barbara, CA). Internet version published in Journal of the ACMS 2004.
- Davenport, Anne A. (1997), "The Catholics, the Cathars, and the Concept of Infinity in the Thirteenth Century", Isis 88 (2).
- Ferreirós, José (2007), written at Basel, Switzerland, Labyrinth of Thought: A History of Set Theory and Its Role in Mathematical Thought, Birkhäuser. ISBN 3-7643-8349-6 Contains a detailed treatment of both Cantor's and Dedekind's contributions to set theory.
- Grattan-Guinness, Ivor (1971), "Towards a Biography of Georg Cantor", Annals of Science 27.
- Grattan-Guinness, Ivor (2000), The Search for Mathematical Roots: 1870–1940, Princeton University Press. ISBN 978-0-691-05858-0
- Gray, Robert (1994), "Georg Cantor and Transcendental Numbers", American Mathematical Monthly 101.
- Hallett, Michael (1986), written at New York, Cantorian Set Theory and Limitation of Size, Oxford University Press. ISBN 0-19-853283-0
- Halmos, Paul (1998, 1960), written at New York & Berlin, Naive Set Theory, Springer. ISBN 3-540-90092-6
- Hill, C. O.; Rosado Haddock, G. E. (2000), written at Chicago, Husserl or Frege? Meaning, Objectivity, and Mathematics, Open Court. ISBN 0-8126-9538-0 Three chapters and 18 index entries on Cantor.
- Johnson, Phillip E. (1972), "The Genesis and Development of Set Theory", The Two-Year College Mathematics Journal 3 (1).
- Meschkowski, Herbert (1983), Georg Cantor, Leben, Werk und Wirkung (George Cantor, Life, Work and Influence, in German), Wieveg, Braunschweig
- Moore, A.W. (1995), "A brief history of infinity", Scientific American 272 (4).
- Penrose, Roger (2004), The Road to Reality, Alfred A. Knopf. ISBN 0-679-77631-1 Chapter 16 illustrates how Cantorian thinking intrigues a leading contemporary theoretical physicist.
- Purkert, Walter; Ilgauds, Hans Joachim (1985), Georg Cantor: 1845–1918, Birkhäuser. ISBN 0-8176-1770-1
- Reid, Constance (1996), written at New York, Hilbert, Springer-Verlag. ISBN 0-387-04999-1
- Rucker, Rudy (2005, 1982), Infinity and the Mind, Princeton University Press. ISBN 0-553-25531-2 Deals with similar topics to Aczel, but in more depth.
- Rodych, Victor (2007), "Wittgenstein's Philosophy of Mathematics", in Edward N. Zalta, The Stanford Encyclopedia of Philosophy.
- Snapper, Ernst (1979), "The Three Crises in Mathematics: Logicism, Intuitionism and Formalism", Mathematics Magazine 524.
- Suppes, Patrick (1972, 1960), written at New York, Axiomatic Set Theory, Dover. ISBN 0-486-61630-4 Although the presentation is axiomatic rather than naive, Suppes proves and discusses many of Cantor's results, which demonstrates Cantor's continued importance for the edifice of foundational mathematics.
- Wallace, David Foster (2003), written at New York, Everything and More: A Compact History of Infinity, W.W. Norton and Company. ISBN 0-393-00338-8
- Weir, Alan (1998), "Naive Set Theory is Innocent!", Mind 107 (428).
 |
ଏହି ଲେଖାଟି ଏକ ଅସଂପୂର୍ଣ୍ଣ ଲେଖା, ଆପଣ ଏହାକୁ ଏଠାରେ ବଦଳାଇ ଉଇକିପିଡ଼ିଆକୁ ଉନ୍ନତ କରିପାରିବେ । |
