ଗଣିତ

ଇଂରାଜୀ ଲିଙ୍କ

https://or.wikipedia.org/wiki/Mathematics

ପରିମାଣ, ଗଠନ, ସ୍ଥାନ ଓ ପରିବର୍ତ୍ତନର ବିଦ୍ୟାକୁ ଗଣିତ କୁହାଯାଏ ।^[୧] ଗଣିତରେ ଆବିଷ୍କାର କରୁଥିବା ଲୋକଙ୍କୁ ଗଣିତଜ୍ଞ କୁହାଯାଏ । ସାଧାରଣ ଜୀବନରେ ଗଣିତର ଅନେକ ଆବଶ୍ୟକତା ରହିଛି, ତେଣୁ ଗଣିତଜ୍ଞଙ୍କ ବ୍ୟତୀତ ଅନ୍ୟମାନେ ମଧ୍ୟ ଏଥିରେ ଗବେଷଣା କରନ୍ତି । ଏବେ, ଅନେକ ସ୍ଥାନରେ ଗଣିତର ଆବଶ୍ୟକତା ରହିଛି । ବ୍ୟବସାୟ, ବିଜ୍ଞାନ, ଇଞ୍ଜିନିୟରିଙ୍ଗ୍, ସ୍ଥାପତ୍ୟ ସବୁଥିରେ ଗଣିତର ଆବଶ୍ୟକତା ରହିଛି । ଗଣିତଜ୍ଞମାନେ ତର୍କ ସାହାଯ୍ୟରେ ସମସ୍ୟା ସମାଧାନ କରିଥାନ୍ତି । ଗଣିତଜ୍ଞମାନେ ଅନେକ ସମୟରେ ଅପସାରଣ ପଦ୍ଧତି ଅବଲମ୍ବନ କରନ୍ତି । ଉପଲବ୍ଧ ସତ୍ୟର ବ୍ୟବହାର କରି ନୂତନ ସତ୍ୟ ଆବିଷ୍କାର କରିବାର ବିଶେଷ ଉପାୟ ହେଉଛି ଅପସାରଣ । ଜଣେ ଗଣିତଜ୍ଞ ପାଇଁ, ଗୋଟିଏ ସତ୍ୟ ଓ ତାହାର କାରଣର ସତ୍ୟତା ଉଭୟ ଜରୁରୀ । ଅପସାରଣ ପଦ୍ଧତି ଅନ୍ୟ ଚିନ୍ତା ଓ ଗାଣିତିକ ଚିନ୍ତା ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ସୃଷ୍ଟି କରେ । ଗଣିତଜ୍ଞମାନେ ବିଭିନ୍ନ ବିଷୟରେ ସମାନତା ଅନୁଧ୍ୟାନ କରି ନୂତନ ସୂତ୍ର ସ୍ଥାପନ କରନ୍ତି । ଗାଣିତିକ ପ୍ରମାଣଦ୍ୱାରା ସେଗୁଡ଼ିକର ସତ୍ୟାସତ୍ୟ ନିର୍ଣୟ କରାଯାଏ । ଗାଣିତିକ ସମସ୍ୟାର ସମାଧାନ ପାଇଁ ବର୍ଷବର୍ଷ ଏପରିକି ଶତାବ୍ଦୀ ମଧ୍ୟ ବିତିଯାଏ । ଉନବିଂଶ ଶତାବ୍ଦୀରେ ଗିସେପ୍ପେ ପିନୋ (୧୮୫୮-୧୯୩୨), ଡେଭିଡ୍ ହିଲ୍‌ବର୍ଟ୍ (୧୮୬୨-୧୯୪୩) ଆଦିଙ୍କ ଉଲ୍ଲେଖନୀୟ କାର୍ଯ୍ୟ ପରେ, ପୂର୍ବପ୍ରମାଣିତ ସୂତ୍ରଦ୍ୱାରା ନୂତନ ସୂତ୍ରପାତ କରିବା ପ୍ରଥା ପ୍ରଚଳିତ ହୋଇଛି । ବାସ୍ତବ ପରିସ୍ଥିତିର ସଠିକ ଗାଣିତିକ ସୂତ୍ର ନିରୂପଣ ହେଲା ପରେ, ଗାଣିତିକ ତର୍କଦ୍ୱାରା ତାହାର ପୂର୍ବାନୁମାନ କରାଯାଇପାରେ ।

ଅପସାରଣ ଓ ତର୍କଦ୍ୱାରା ଗଣିତ ଗଣନ, ହିସାବ, ମାପ ଓ ଭୌତିକ ବସ୍ତୁର ଆକୃତି ଓ ଗତି ବିଷୟରେ ତଥ୍ୟ ପ୍ରଦାନ କରେ । ଅତି ପୁରାତନ କାଳରୁ ଗଣିତର ଉତ୍ପତ୍ତି ହୋଇସାରିଥିଲା । ଗ୍ରୀକ୍ ଗଣିତରେ ପ୍ରଥମେ କଠିନ ଯୁକ୍ତି ହୋଇଥିବାର ଜଣାଯାଏ, ଉଲ୍ଲେଖନୀୟ ଭାବେ ୟୁକ୍ଲିଡ୍‌ଙ୍କର ଏଲିମେଣ୍ଟ୍‌ସ୍‌ରେ (Elements) । ପ୍ରଥମରୁ ଅପେକ୍ଷାକୃତ ଧିର ଗତିରେ ଉନ୍ନତି କରୁଥିବା ଗଣିତ, ରେନେସାଁ ଯୁଗରେ ବିଜ୍ଞାନର ଅନ୍ୟାନ୍ୟ ଆବିଷ୍କାର ସହିତ ମିଶି ବେଗବାନ ହେଲା, ଯାହା ଏବେ ପର୍ଯ୍ୟନ୍ତ ଅବ୍ୟାହତ ଅଛି ।

ସାଧାରଣ ଧାରଣା

ଗଣିତରେ ଏ ସବୁ ଥାଏ:

ସଂଖ୍ୟା (ଉଦାହରଣ ୩+୬=୯)
ଗଠନ: ବସ୍ତୁମାନେ କେମିତି ସଂଗଠିତ
ସ୍ଥାନ: ବସ୍ତୁର ଅବସ୍ଥିତି ଓ ସଜାଣି
ପରିବର୍ତ୍ତନ: ସମୟ ସହିତ ବସ୍ତୁରେ ବଦଳ

ସଂଖ୍ୟା

ଗଣିତରେ ସଂଖ୍ୟା ବା ପରିମାଣର ଅଧ୍ୟୟନ ଥାଏ ।^[୩]

$1,2,3,\ldots$	$\ldots ,-1,0,1,\ldots$	${\frac {1}{2}},{\frac {2}{3}},0.125,\ldots$	$\pi ,e,{\sqrt {2}},\ldots$	$1+i,2e^{i\pi /3},\ldots$
ଗଣନ ସଂଖ୍ୟା	ପୂର୍ଣ ସଂଖ୍ୟା	ପରିମେୟ ସଂଖ୍ୟା	ବାସ୍ତବ ସଂଖ୍ୟା	ଜଟିଳ ସଂଖ୍ୟା
	$\omega ,\omega +1,\ldots ,2\omega ,\ldots$	$\aleph _{0},\aleph _{1},\ldots$	$+,-,\times ,\div$	$>,\geq ,=,\leq ,$	$f(x)={\sqrt {x}}$
	ପୂରଣବାଚକ ସଂଖ୍ୟା	ଅଙ୍କବାଚକ ସଂଖ୍ୟା	ପାଟୀଗଣିତ ପ୍ରକ୍ରିୟା	ଗାଣିତିକ ସମ୍ବନ୍ଧ	ଫଳନ

ଗଠନ

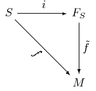
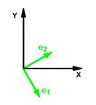
ଗଣିତର କେତେକ ଶାଖା ବସ୍ତୁର ଗଠନ ଉପରେ ଅଧ୍ୟୟନ କରନ୍ତି ।


ସଂଖ୍ୟା ତତ୍ତ୍ୱ	ବୀଜଗଣିତ ସାର	ରୈଖିକ ବୀଜଗଣିତ	କ୍ରମ ସିଦ୍ଧାନ୍ତ	ଲେଖ ତତ୍ତ୍ୱ

ଆକୃତି

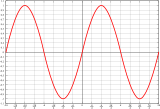
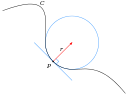
ଗଣିତର କେତେକ ଶାଖା ବସ୍ତୁର ଆକୃତି ଉପରେ ଅଧ୍ୟୟନ କରନ୍ତି ।


ସଜାଣି	ଜ୍ୟାମିତି	ତ୍ରିକୋଣମିତି	ଅନ୍ତର ଜ୍ୟାମିତି	ଭଗ୍ନ ଜ୍ୟାମିତି

ପରିବର୍ତ୍ତନ

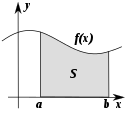
ଗଣିତର କେତେକ ଶାଖା ବସ୍ତୁର ପରିବର୍ତ୍ତନ ପ୍ରଣାଳୀ ଉପରେ ଅଧ୍ୟୟନ କରନ୍ତି ।


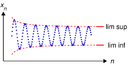
ପଥରି	ଭେକ୍ଟର୍ ପଥରି	ବିଶ୍ଳେଷଣ

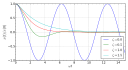
	ବିଭେଦକ ସମୀକରଣ	ଗତିଜ ତନ୍ତ୍ର	ବିଶୃଙ୍ଖଳା ତତ୍ତ୍ୱ

ଗାଣିତିକ ଉପକରଣ

ଗାଣିତିକ ସମସ୍ୟାର ସମାଧାନ ପାଇଁ ବ୍ୟବହୃତ ଉପକରଣ ।

ପୁରୁଣା

ଆବାକସ୍
ଆଦେଶ ସଂଚାଳନ କାଲ୍‌କୁଲେଟର୍
ନାପିୟରଙ୍କ ହାଡ଼
ରୁଲର୍ ଓ କମ୍ପାସ୍
ମାନସାଙ୍କ ହିସାବ

ନୂଆ

କାଲ୍‌କୁଲେଟର୍ ଓ କମ୍ପ୍ୟୁଟର୍
ପ୍ରୋଗ୍ରାମିଙ୍ଗ୍ ଭାଷା
କମ୍ପ୍ୟୁଟର୍ ବୀଜଗଣିତ ତନ୍ତ୍ର
ଇଣ୍ଟର୍‌ନେଟ୍ ସର୍ଟ୍‌ହାଣ୍ଡ୍ ସଂକେତ
ପରିସଂଖ୍ୟାନ ବିଶ୍ଳେଷଣ ସଫ୍ଟ୍‌ୱେର୍
- SPSS
- SAS ପ୍ରୋଗ୍ରାମିଙ୍ଗ୍ ଭାଷା
- R ପ୍ରୋଗ୍ରାମିଙ୍ଗ୍ ଭାଷା

ଆଧାର

↑ "mathematics, n. : Oxford English Dictionary Oxford English Dictionary. Oxford University Press. 2012. Archived from the original on November 16, 2019. Retrieved June 16, 2012. "The science of space, number, quantity, and arrangement, whose methods involve logical reasoning and usually the use of symbolic notation, and which includes geometry, arithmetic, algebra, and analysis."". web.archive.org. 2019-11-16. Archived from the original on 2019-11-16. Retrieved 2022-01-15.{{cite web}}: CS1 maint: bot: original URL status unknown (link)
↑ "Egyptian Mathematical Papyri - Mathematicians of the African Diaspora". web.archive.org. 2015-04-07. Retrieved 2022-01-15.
↑ "number, n. : OED Online. Oxford University Press. Archived from the original on 2018-10-04. Retrieved 2017-05-16". web.archive.org. 2018-10-04. Archived from the original on 2018-10-04. Retrieved 2022-01-15.{{cite web}}: CS1 maint: bot: original URL status unknown (link)

[1] "mathematics, n. : Oxford English Dictionary Oxford English Dictionary. Oxford University Press. 2012. Archived from the original on November 16, 2019. Retrieved June 16, 2012. "The science of space, number, quantity, and arrangement, whose methods involve logical reasoning and usually the use of symbolic notation, and which includes geometry, arithmetic, algebra, and analysis."". web.archive.org. 2019-11-16. Archived from the original on 2019-11-16. Retrieved 2022-01-15.{{cite web}}: CS1 maint: bot: original URL status unknown (link)

[2] "Egyptian Mathematical Papyri - Mathematicians of the African Diaspora". web.archive.org. 2015-04-07. Retrieved 2022-01-15.

[3] "number, n. : OED Online. Oxford University Press. Archived from the original on 2018-10-04. Retrieved 2017-05-16". web.archive.org. 2018-10-04. Archived from the original on 2018-10-04. Retrieved 2022-01-15.{{cite web}}: CS1 maint: bot: original URL status unknown (link)

[୧]

[୨]

[୩]